Simplified Hypercube
Representation.
For Binary Spaces
John L. Sokol, April 27, 2001
Developed by John Sokol 1999
for use in visualizing Error correction code space.
Please excuse the graphics;
these are just a quick and dirty drawing to get the point across.
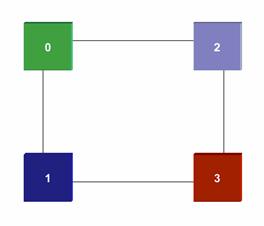
2-dimensional cube (Square)
This Image is from Page 9 from "In Search of a 7D Hypercube".
What we are calling a hypercube is actually a binary space. By that I mean there is no interior dimensions to the cube or of the lines interconnecting the cube, there are just 2 nodes at each end of a line, this is a binary 0 and 1 there are no points in-between. In a true multidimensional square, cube and hypercube there is a volume there with the space.
With this notation a node is 0 or 1 so a
00 – 10 0 - 2
| |
= | |
01 – 11 1 - 3
Binary Decimal
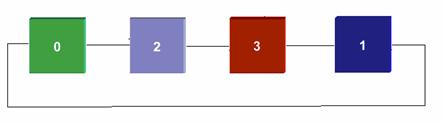
Flattened, 2-dimensional cube (Square)
Because of this lack of interior dimensions it becomes possible to smash a 2-dimentional square into a 4-node line. See image above.
This then flattens to 0 - 2 - 3 - 1 - Wrap Around to 0
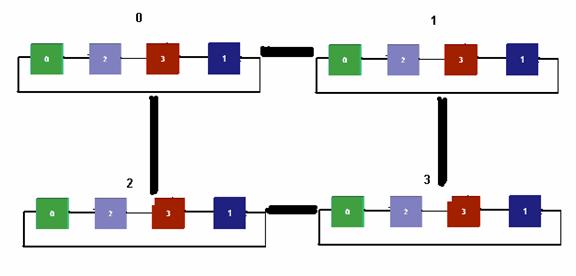
4 Dimensional Hypercube made of a square of squares
4 Dimensional Hypercube made of a square of squares in the flatten notation.
Coordinates and Distance can be given in binary or distorted Cartesian coordinates.
In X,Y notation the top right node would be (1,0) decimal or 0100 binary. The next node down would be (1,2) decimal and 0110 binary.
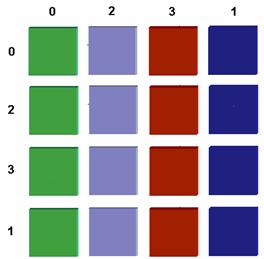
0, 8,12, 4 0000, 1000, 1100, 0100
2,10,14, 6 0010, 1010, 1110, 0110
3,11,15, 7 0011, 1011, 1111, 0111
1, 9,13, 5 0001, 1001, 1101, 0101
Decimal Binary.
Visible and Node distances are equivalent to hamming distance in binary number space.
This can then done recursively over and over to increase dimensions endlessly without becoming the unintelligible mess that other methods tend to end up as.
The distances and paths are still visible..
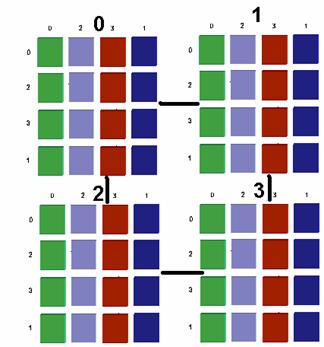
6 Dimensional Hypercube made of a 4 hypercubes in a square..

8 Dimensional Hypercube made of a hypercube of hypercubes.
Whacking this drawing in half either vertically or horizontally can make a seven dimensional hypercube.